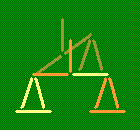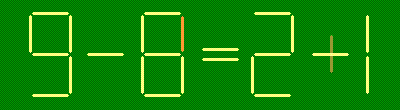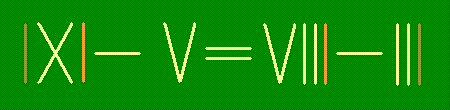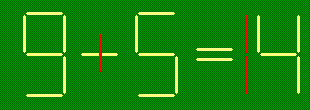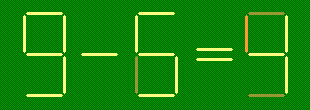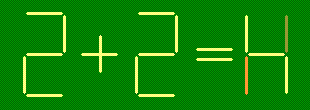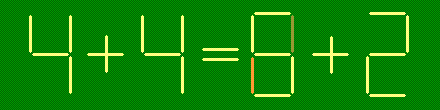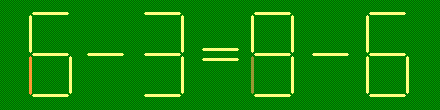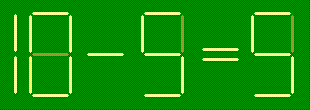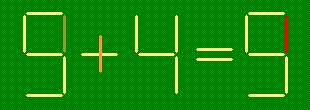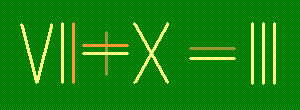МАЛЫЙ МЕХМАТ МГУ

Кружок 7 класса
2009/2010 учебный год
Занятие 21. Зубочистки!!!
Для решения задач этого занятия школьникам было предложено принести с собой зубочистки (традиционные спички запретила пожарная охрана МГУ). Задачи этого занятия были разделены на два варианта, в каждом варианте — по четыре раздела.
I. Фигуры из зубочисток
Вариант 1
- 1.
-
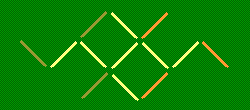
Рак. Рак из зубочисток ползет вверх. Переложите три зубочистки так, чтобы он полз вниз.

- 2.
-
Весы. Весы составлены из девяти зубочисток и не находятся в положении равновесия. Переложите пять зубочисток так, чтобы весы были в равновесии.
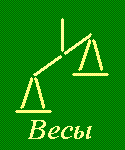
- 3.
-
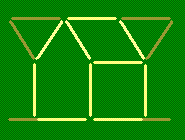
Храм. Этот греческий храм построен из одиннадцати зубочисток. Переложите четыре зубочистки так, чтобы получилось пятнадцать квадратов.
 Решение. Переложив зубочистки так, как показано на этом рисунке, мы получим 15 квадратов: 9 совсем маленьких квадратиков, четыре квадрата побольше (каждый из них состоит из четырех маленьких квадратиков) и два больших квадрата.
Решение. Переложив зубочистки так, как показано на этом рисунке, мы получим 15 квадратов: 9 совсем маленьких квадратиков, четыре квадрата побольше (каждый из них состоит из четырех маленьких квадратиков) и два больших квадрата.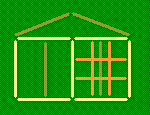
- 4.
-
Бокал. Внутри бокала из четырех зубочисток находится монета. Не трогая монету, переложите две зубочистки так, чтобы монета оказалась снаружи такого же бокала.

- 5.
-
Восемь прямых углов. Можно ли пятью зубочистками образовать восемь прямых углов? Зубочистки могут касаться друг друга только концами.
Решение. Надо сначала выложить из четырех зубочисток крест (это уже четыре прямых угла), а потом пятую зубочистку поставить вертикально в центре этого креста (она образует еще четыре прямых угла с зубочистками, лежащими на столе). Правда, вряд ли вам удастся это сделать без помощи пластилина.
Вариант 2
- 1.
-
Дом. Переложите две зубочистки так, чтобы дом повернулся другой стороной.

- 2.
-
Два бокала составлены из 10 зубочисток. Переложите шесть зубочисток так, чтобы получился дом из задачи №1.

- 3.
-
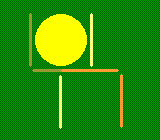
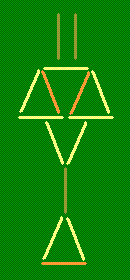
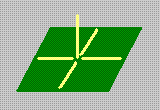
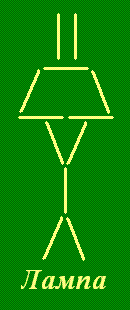
Лампа. В лампе переложите три зубочистки так, чтобы получилось пять равных треугольников.
- 4.
-
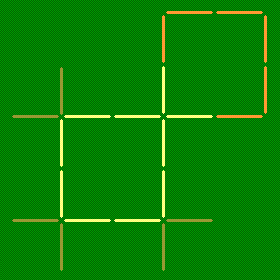
Два квадрата. В фигуре, изображенной на рисунке, переложите шесть зубочисток так, чтобы получилось два квадрата.

- 5.
-
Можно ли из шести зубочисток составить четыре равносторонних треугольника?
Решение. Для этого нужно сложить вот такую пирамидку (у нее четыре треугольных грани). Правда, сделать это без помощи пластилина вам вряд ли удастся.

II. Числа из зубочисток
Числа из зубочисток можно выкладывать, используя арабские или римские цифры. В некоторых задачах нужно выкладывать из зубочисток слова-числительные.
Многие задачи этого раздела имеют много различных решений просто потому, что их условия можно понимать очень по-разному. На занятии школьниками было предложено немало различных решений, многие из которых были признаны правильными (хотя и не совпадали с авторскими). К сожалению, у нас нет возможности привести их все здесь, поэтому мы приводим лишь авторские решения. К решениям даются соответствующие пояснения.
Вариант 1
- 1.
-
Можно ли сделать:
- а)
- из десяти три?
- б)
- из девяти сто?
Решение. Имелось в виду, что надо из указанного количества зубочисток сложить указанные числа. Пункт б) имеет два решения: из девяти спичек можно выложить как число 100, так и слово «сто».
- 2.
-
Как сделать:
- а)
- из двух пять?
- б)
- из трех четыре?
- в)
- из трех шесть?
- г)
- из четырех семь?
Решение. Нужно сложить указанные числа из указанного количества зубочисток, используя римские цифры: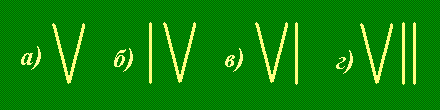
- 3.
-
Можно ли разделить пополам:
- а)
- девять и получить четыре?
- б)
- двенадцать и получить семь?
Решение. Нужно сложить указанные числа из зубочисток при помощи римских цифр так, как показано на рисунке, а затем отделить верхнюю половину каждого числа от нижней. Верняя половина от IX равна IV, верхняя половина от XII равна VII.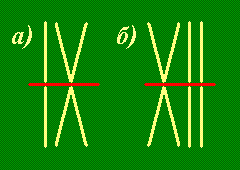
- 4.
-
Как это так:
- а)
- девять без двух — четыре?
- б)
- восемнадцать без пяти — десять?
Решение. Нужно выложить соответствующие числа (арабскими или римскими цифрами) из зубочисток и убрать нужное количество зубочисток, чтобы получить новые числа.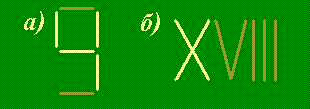
- 5.
-
Как это так:
- а)
- пять да один — четыре?
- б)
- два да два — восемь?
- в)
- пять да два — пятнадцать?
Решение. В этой задаче нужно выложить из зубочисток соответствующие числа, а потом, добавив к ним нужное число зубочисток, получить новые числа.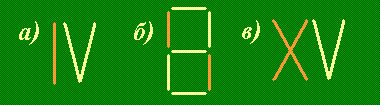
- 6.
-
Какое это число: если от него один отнимается, оно одним увеличивается?
Решение. Таким свойством обладают многие числа, выложенные из зубочисток при помощи римских цифр: если убрать одну зубочистку, число увеличивается на единицу. На рисунке показано два примера, а вы можете придумать много других самостоятельно.
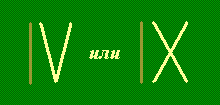
- 7.
-
Уменьшить вдвое. Из восьми зубочисток сложено число 10 (см. рисунок). Переложив одну зубочистку, уменьшите это число в два раза.
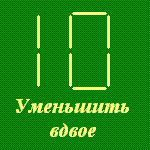 Решение. Здесь несколько непривычным способом выложена из зубочисток пятерка, к тому же положенная набок.
Решение. Здесь несколько непривычным способом выложена из зубочисток пятерка, к тому же положенная набок.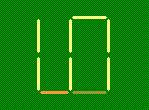
Вариант 2
- 1.
-
Можно ли сделать:
- а)
- из четырнадцати семь?
- б)
- из девяти три?
Решение. Имелось в виду, что надо из указанного количества зубочисток выложить словами указанные числа (см. рисунок).
- 2.
-
Как сделать:
- а)
- из двух десять?
- б)
- из пяти шесть?
- в)
- из пяти четыре?
- г)
- из шести десять?
Решение. Нужно сложить указанные числа из указанного количества зубочисток, используя римские цифры: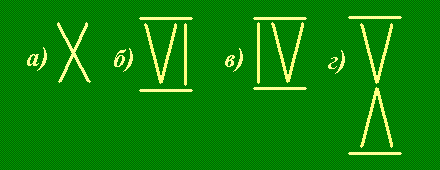
- 3.
-
Можно ли разделить пополам:
- а)
- 11 и получить 6?
- б)
- 18 и получить 10?
Решение. Нужно сложить указанные числа из зубочисток при помощи римских или арабских цифр так, как показано на рисунке, а затем отделить верхнюю половину каждого числа от нижней. Верняя половина от XI равна VI, верхняя половина от 18 равна 10. Правда, в числе 18 восьмерка не совсем обычная: в середине у нее «перекладина» из двух зубочисток, а не из одной, как это обычно бывает.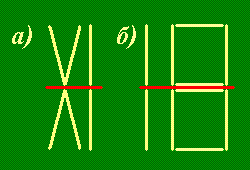
- 4.
-
Как это так:
- а)
- восемь без трех — четыре?
- б)
- восемнадцать без трех — семь?
Решение. Нужно выложить соответствующие цисла (арабскими или римскими цифрами) из зубочисток и нужное количество зубочисток убрать, чтобы получить новые числа.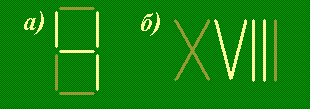
- 5.
-
Как это так:
- а)
- пять да два — пятнадцать?
- б)
- ноль да один — восемь?
- в)
- два да один — шесть?
Решение. В первых двух пунктах этой задачи нужно выложить из зубочисток соответствующие числа, а потом, добавив к ним нужное число зубочисток, получить новые числа. В последнем пункте нужно из двух зубочисток сложить римскую цифру V, а потом при помощи еще одной зубочистки сделать из нее цифру VI.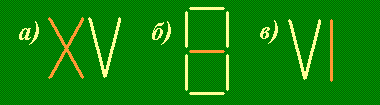
- 6.
-
Какое это число: если один у него переставляется, оно двумя увеличивается?
Решение. Эта задача решается при помощи римских цифр. Можно, например, выложить из зубочисток число IV и превратить его в VI, переложив одну зубочистку (см. рисунок).
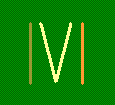
- 7.
-
Из двух квадратов пять. Из одиннадцати зубочисток сложены два квадрата (см. рисунок). Сделайте пять, переложив одну зубочистку и убрав две.
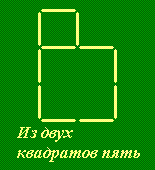 Решение. Конечно, в условии этой задачи слово «пять» означает не «пять квадратов», а число 5 (подсказка содержится в названии раздела). Здесь несколько непривычным образом выложена из зубочисток пятерка:
Решение. Конечно, в условии этой задачи слово «пять» означает не «пять квадратов», а число 5 (подсказка содержится в названии раздела). Здесь несколько непривычным образом выложена из зубочисток пятерка: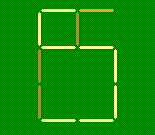
III. Равенства из зубочисток
Вариант 1
- 1.
-
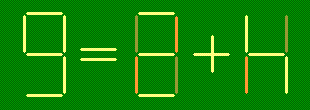
Из зубочисток сложены верные равенства. Получите из них новые верные равенства
- а)
- переложив одну зубочистку:
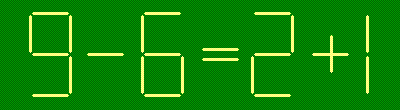
- б)
- переложив две зубочистки:
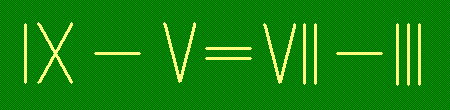
- в)
- добавив три зубочистки:
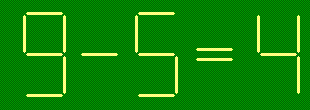
- г)
- убрав две зубочистки и переложив одну:
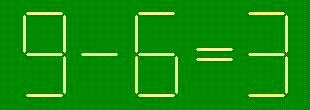
- д)
- переложив одну зубочистку:
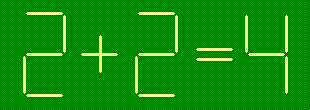
- 2.
-
Исправьте неверное равенство, переложив одну зубочистку.
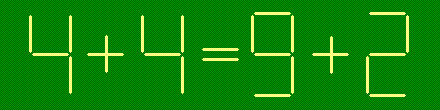
Вариант 2
- 1.
-
Из зубочисток сложены верные равенства. Получите из них новые верные равенства
- а)
- переложив одну зубочистку:
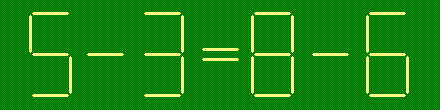
- б)
- переложив две зубочистки:
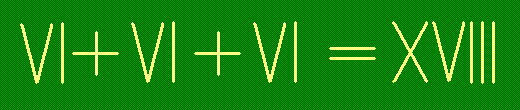
- в)
- убрав три зубочистки:
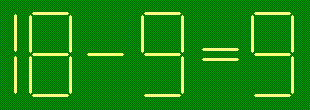
- г)
- добавив одну зубочистку и переложив одну:
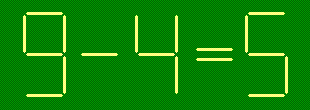
- д)
- переложив три зубочистки:
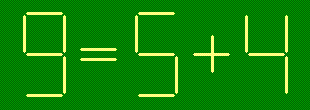
- 2.
-
Исправьте неверное равенство, переложив две зубочистки.
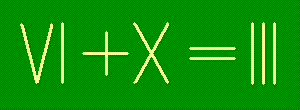
IV. Игры с зубочистками
Первая задача этого раздела предлагалась в обоих вариантах, вторая — только в первом, а третья — только во втором.
- 1.
-
Пятнадцать зубочисток расположены в ряд. Требуется собрать их в пять кучек по три зубочистки, перекладывая их по одной и каждый раз перескакивая при этом через три зубочистки.
Решение. Обозначим положенные в ряд зубочистки номерами 1, 2, …, 15. Задача решается следующими перекладываниями: 2 к 6, 1 к 6, 8 к 12, 7 к 12, 9 к 5, 10 к 5, 4 между 5 и 6, 3 между 5 и 6, 11 между 5 и 6, 13 на место №11, 14 на то же место, 15 на то же место.
- 2.
-
Десять зубочисток положены в один ряд параллельно друг другу. Сделайте из них пять крестов, переложив пять зубочисток, причем так, чтобы каждая из них, прежде чем занять свое место, была перенесена ровно через две зубочистки, считая и те, которые уже образуют крест.
Решение. Ниже изображена последовательность перекладываний, приводящая к требуемому результату. Символ «|» означает отдельно лежащую зубочистку, символ «+» — две зубочистки, образующие крест; символ «_» указывает на то место, с которого была взята только что переложенная зубочистка, а жирным выделены только что образованные кресты.
| | | | | | | | | | + | | _ | | | | | | + | + | | _ | | | + | + _ | | + | + _ + + | + | + + + + + _ - 3.
-
На столе лежат в ряд параллельно друг другу четыре зубочистки, чередующиеся с четырьмя половинками (см. рисунок). Переложите их так, чтобы сначала лежали четыре половинки, а затем четыре целых зубочистки. При этом разрешается перекладывать только по две рядом лежащие зубочистки, сохраняя расстояние между ними.
 Решение. Пронумеруем лежащие зубочистки и их половинки в порядке следования слева направо номерами 1, 2, …, 8. Номерами 9 и 10 снабдим два пустых места после зубочистки №8. Перекладываем: 2 и 3 на 9 и 10; 5 и 6 на 2 и 3; 8 и 9 на 5 и 6; 1 и 2 на 8 и 9.
Решение. Пронумеруем лежащие зубочистки и их половинки в порядке следования слева направо номерами 1, 2, …, 8. Номерами 9 и 10 снабдим два пустых места после зубочистки №8. Перекладываем: 2 и 3 на 9 и 10; 5 и 6 на 2 и 3; 8 и 9 на 5 и 6; 1 и 2 на 8 и 9.