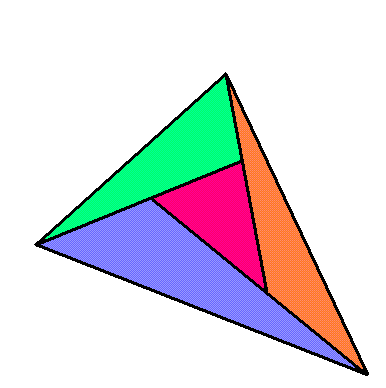МАЛЫЙ МЕХМАТ МГУ

Кружок 7 класса

Занятие 10. Математический футбол

Правила

1. В игре участвуют 2 команды. Каждая команда состоит из вратаря, защитников и нападающих.
2. В качестве решения задачи принимается только ответ, без пояснений.
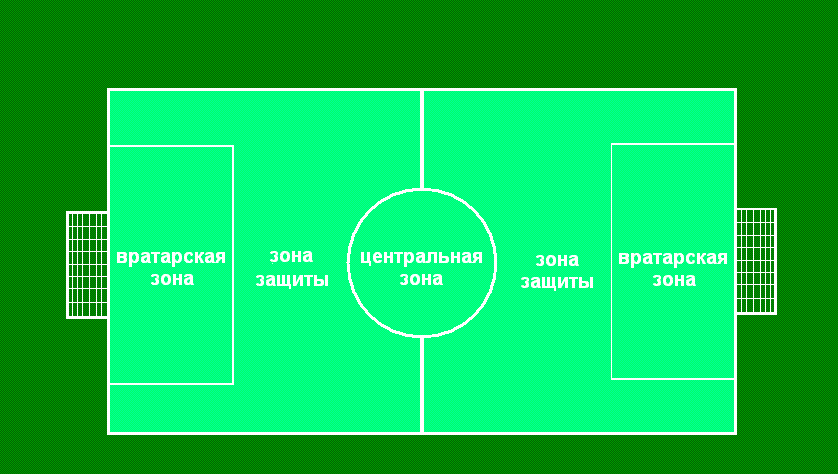
3. Поле делится на пять зон:
   1. центральная зона — для вбрасывания мяча.
   2. две зоны защиты, где играют защитники одной команды и нападающие другой.
   3. 2 вратарские зоны, где играет один вратарь и нападающие противоположенной команды.





4. В начале игры происходит «вбрасывание мяча». Все члены команды сидят на местах, читается условие задачи. Как только кто-то решает задачу, он поднимает руку и с разрешения ведущего говорит ответ. Неправильный ответ одной команды равносилен тому, что правильный ответ дала другая команда. Если команда дала правильный ответ, то к доске выходят нападающие этой команды и защитники другой. Теперь ответ давать могут только те, кто играет у доски. Читается следующая задача. Если побеждают нападающие, то мяч переходит во вратарскую зону, и вместо защитников второй команды выходит вратарь. Если побеждают защитники, то мяч переходит в зону защиты соперников, и команды меняются ролями: вместо защитников выходят нападающие, вместо нападающих защитники. Если во вратарской зоне вратарь дает неправильный ответ, или правильный ответ дают нападающие, то атакующая команда забила гол. Мяч перемещается в центральную зону, происходит вбрасывание. В противном случае мяч перемещается в зону защиты обороняющейся команды, и вместо вратаря снова выходят защитники.
5. За нарушение дисциплины команда наказывается пенальти: вратарь провинившейся команды играет против одного из игроков другой команды по тем же правилам, по которым обычно происходит игра во вратарской зоне.

Задачи

1.

Маша и Катя весят вместе 40 кг, Катя и Света весят вместе 50 кг, Света и Даша – 60 кг, Даша и Галя – 70 кг, Маша и Галя – 80 кг. сколько весит каждая из девочек?

Ответ

Ответ. Даша весит 20 кг, Маша – 30 кг, Света – 40 кг, Катя – 10 кг, Галя – 50 кг.

2.

Решите ребус: ЧАЙ:АЙ=5.

Ответ

Ответ. 125:25=5, 375:75=5, 250:50=5.

3.

Принесли пять чемоданов и пять ключей от них. Укажите наименьшее число проб, достаточных для того, чтобы подобрать ключ к каждому из них?

Ответ

Ответ. 10 проб

4.

За мороженым стоят Юра, Ира, Оля, Саша и Коля. Юра стоит раньше Ирины, но после Коли. Оля и Коля не стоят рядом, а Саша не находится рядом ни с Колей, ни с Юрой, ни с Олей. В каком порядке стоят ребята?

Ответ

Ответ. Коля, Юра, Оля, Ирина, Саша.

5.

По какой цене за кг нужно продавать смесь конфет «Солнышко» и «Луна», если цена «Солнышка» 50 рублей за кг, цена «Луны», — 70 рублей, и в смеси «Луны» втрое больше, чем «Солнышка»?

Ответ

Ответ. по 65 руб. за кг.

6.

Пете выставили годовые оценки по 12 предметам. Его средний балл оказался равен 3,5. По скольким предметам ему надо повысить свои оценки на 1 балл, чтобы средний балл стал равен 4?

Ответ

Ответ. по 6 предметам.

7.

Какой угол образуют часовая и минутная стрелки в двадцать минут первого?

Ответ

Ответ. 110 градусов.

8.

В двух коробках 74 книги. В одной из них 2/19 не по математике, а в другой 5/9 с синей обложкой. (Все книги целые!) Сколько книг в каждой из коробок?

Ответ

Ответ. 38 и 36 книг.

9.

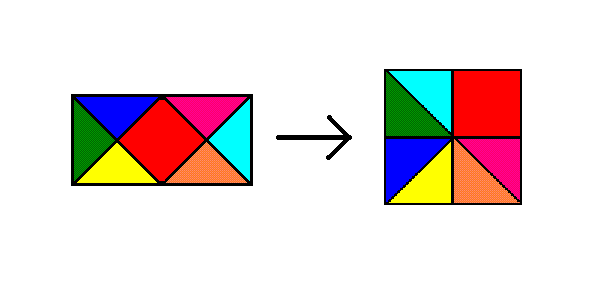
Разрежьте прямоугольник 2×1 на 7 частей, из которых можно составить квадрат.

Ответ

Ответ.

10.

Приведите пример географической карты, на которой четыре треугольные страны граничат каждая с каждой.

Ответ

Ответ.

11.

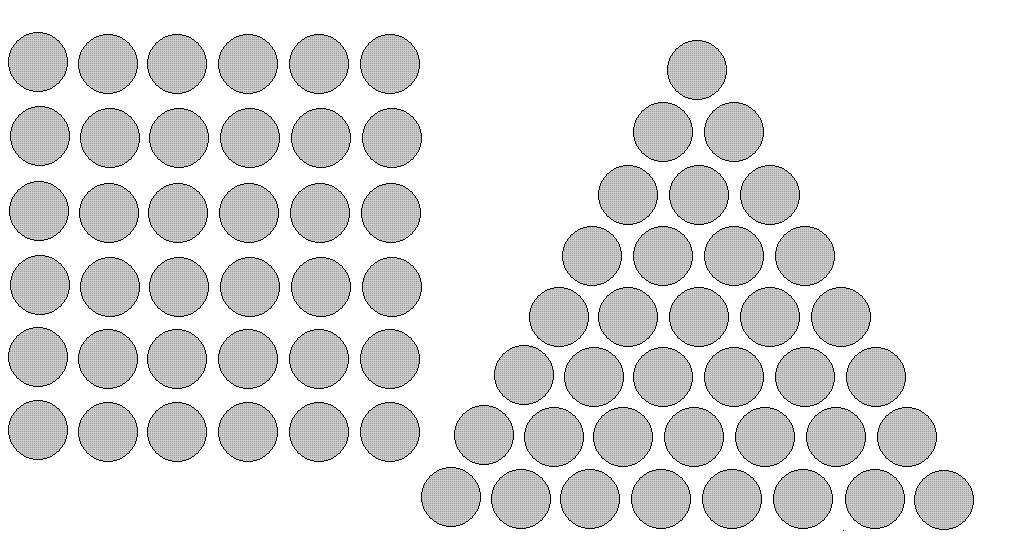
15 одинаковых шариков можно сложить в виде треугольника, но нельзя сложить в виде квадрата — одного шарика не хватает. Из какого количества шариков, не превосходящего 50, можно сложить как треугольник, так и квадрат?

Ответ

Ответ. 1 и 36=6×6=1+2+3+4+5+6+7+8.

12.

Расставьте по кругу четыре единицы, три двойки и три тройки так, чтобы сумма любых трех подряд стоящих цифр не делилась на 3.

Ответ

Ответ. 11311223322 (возможны варианты).

13.

Квадрат со стороной длины 1 метр разрезали на квадраты со стороной 4 см и выложили в ряд. Найдите длину ряда.

Ответ

Ответ. 25 м.

14.

У Саши есть 4 карточки с цифрами 1, 2, 3 и 4. Он составляет из них трёхзначные числа. Сколько различных чисел, делящихся на 6, он может получить?

Ответ

Ответ. 6.

15.

Какое наименьшее число детей может быть в семье, если у каждого ребёнка есть хотя бы 1 сестра и хотя бы 1 брат?

Ответ

Ответ. 4.

16.

В нашей компании 5 человек. У нас есть некоторое количество денег, в среднем по 8 рублей на человека. У меня 10 рублей. Сколько в среднем денег у остальных четырёх членов компании?

Ответ

Ответ. 7,5 руб.

17.

Сумма возрастов нескольких друзей 29 лет. Через 3 года сумма их возрастов стала 41. Сколько всего друзей?

Ответ

Ответ. 4.

18.

Один множитель увеличили на 10%, второй уменьшили на 10%. На сколько процентов и в какую сторону изменилось произведение?

Ответ

Ответ. Уменьшилось на 1%.

19.

Найдите последнюю цифру произведения всех нечётных чисел от 1 до 99.

Ответ

Ответ. 5.

20.

Найдите наименьшее десятизначное число, в записи которого все цифры разные.

Ответ

Ответ. 1023456789.

21.

Жан-Кристофф изучает русский язык. Он записал некоторое трёхзначное число сначала цифрами, а потом — словами по-русски. Оказалось, что все цифры различны и идут в порядке возрастания, а все слова начинаются с одной и той же буквы. Какое число он записал?

Ответ

Ответ. 147.

22.

Сторона квадратной изгороди 10 метров. Через каждые 2 метра, начиная с угла, стоит столбик. Сколько всего столбиков в изгороди?

Ответ

Ответ. 20.

23.

У продавца было два куска ткани по 36 м. Он продал ткань кусками по 3 м. Сколько раз ему пришлось резать ткань?

Ответ

Ответ. 22.

24.

Просидев первую половину урока, Петя уснул и проснулся, когда до конца осталось половина того, что он проспал. Какую часть урока он проспал?

Ответ

Ответ. Одну треть.

25.

Винни-Пуху подарили бочонок с мёдом весом 7 кг. Когда он съел половину мёда, бочонок стал весить 4 кг. Сколько весил пустой бочонок?

Ответ

Ответ. 1 кг.

26.

Антоше подарили весы и он стал взвешивать всё подряд. Вес машины оказался равным весу мяча и двух кубиков, вес машины и кубика — весу двух мячей. Сколько кубиков уравновесят машину?

Ответ

Ответ. 5 кубиков.

27.

Малыш съедает банку варенья за 6 минут, а Карлсон — в 2 раза быстрее. За какое время они съедят 3 банки варенья?

Ответ

Ответ. 6 минут.

28.

Вася пошёл с папой в тир. Папа разрешил ему сделать 5 выстрелов, а за каждое попадание — ещё по 2 выстрела. Всего Вася сделал 25 выстрелов. Сколько раз он попал в цель?

Ответ

Ответ. 10.

29.

В ряд выписали числа от 40 до 60. Сколько раз встретилась цифра 5?

Ответ

Ответ. 12.

30.

Однажды царь наградил крестьянина яблоком из своего сада. Пришёл крестьянин и видит: сад огорожен тремя заборами, и в каждом ворота. Подошел крестьянин к первому сторожу и показал царский указ, а сторож ему в ответ: «Иди и возьми, но при выходе отдашь мне половину тех яблок, что будешь нести, да ещё одно». Это же сказали ему второй и третий сторожа. Сколько яблок должен взять крестьянин, чтобы после расплаты с бдительными сторожами у него осталось одно яблоко?

Ответ

Ответ. 22 яблока.

31.

Найдите четыре последовательных чётных числа, сумма которых равна 4052.

Ответ

Ответ. 1010, 1012, 1014, 1016.

32.

Найдите семь таких идущих подряд целых чисел, что сумма трёх первых равна сумме четырёх последних.

Ответ

Ответ. -15, -14, -13, -12, -11, -10, -9.

33.

Какова максимальная возможная разность между трехзначным числом и суммой его цифр?

Ответ

Ответ. 972=999-27.

34.

Расставьте в записи 4×12+18:6+3 скобки так, чтобы получился наименьший возможный результат.

Ответ

Ответ. (4·12+18):(6+3)=22/3.

Примечание: На занятии игра проводилась не по всем задачам. В разных аудиториях предлагались разные задачи из приведенного выше списка (примерно 10–15 штук) исходя из ограничений по времени.