МАЛЫЙ МЕХМАТ МГУ

Кружок 7 класса

Занятие 20. Меренье земли и тортов

1.

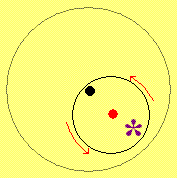
На 23 февраля девочки 7«Б» класса решили подарить мальчикам большой торт. Они замесили тесто и сделали из него круглые коржи. На верхнем корже они хотели написать «С 23 февраля!» черничным соком, но только капнув, увидели, что сок растекся в красивую звездочку, и девочки решили ее поместить в центр. Смогут ли они это сделать, разрезав корж на 3 части?

Ответ Решение

Ответ. Да, смогут.

Решение. Нужно вырезать из верхнего коржа две одинаковые круглые части, в центре одной из которых помещается звездочка, а центр другой совпадает с центром всего коржа (см. рисунок). После этого эти части нужно поменять местами.

2.

У Витали есть 4 одинаковые спички. Он составил из них четырехугольник. Обязательно ли это квадрат?

Ответ Решение

Ответ. Не обязательно.

Решение. Это может быть и ромб, не являющийся квадратом (например, такой, как в задаче №4).

3.

У Насти есть кусок красивой ленты длиной 144 см. Она хочет отрезать от него 2 куска длиной 27 см, чтобы заплести косички. Как ей это сделать, если у нее нет линейки?

Решение

Решение. Заметим, что 144:16=9. Поэтому отмерить кусок длиной 9 см можно, сложив ленту пополам четыре раза (2⁴=16). Затем нужно просто отмерить три таких куска, в результате получится кусок длиной 27 см. После этого второй кусок получить совсем легко.

4.

Коля ждал, пока школьники решат задачки, и сложил из четырех зубочисток ромб, у которого одна из диагоналей была равна его стороне. Какие углы у этого ромба?

Ответ Решение

Ответ. 60°, 120°, 60°, 120°.

Решение. Диагональ, равная стороне ромба, делит его на два равносторонних треугольника. Острые углы ромба совпадают с углами этих треугольников, а значит, равны 60°. А каждый из тупых углов ромба получается как сумма двух углов треугольников, поэтому равен 60°+60°=120°.

5.

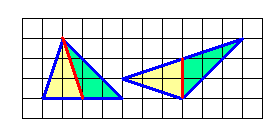
После поедания торта из первой задачи осталось несколько кусочков, которые раздали мальчишкам, чтобы они угостили своих родителей. У Олега есль коробка такой формы, как треугольник на левом рисунке, и кусок торта такой формы, как треугольник на правом рисунке. Как ему разрезать этот кусок только на 2 части, чтобы уложить его в коробку?

Ответ

Ответ.

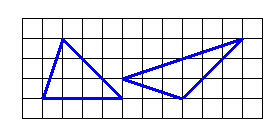
6.

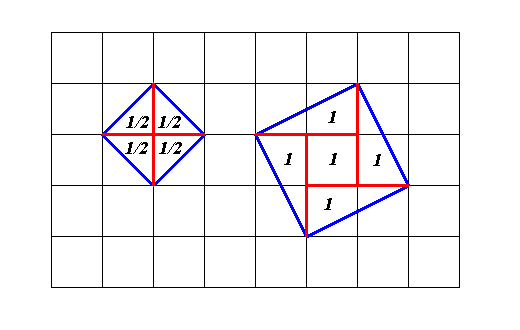
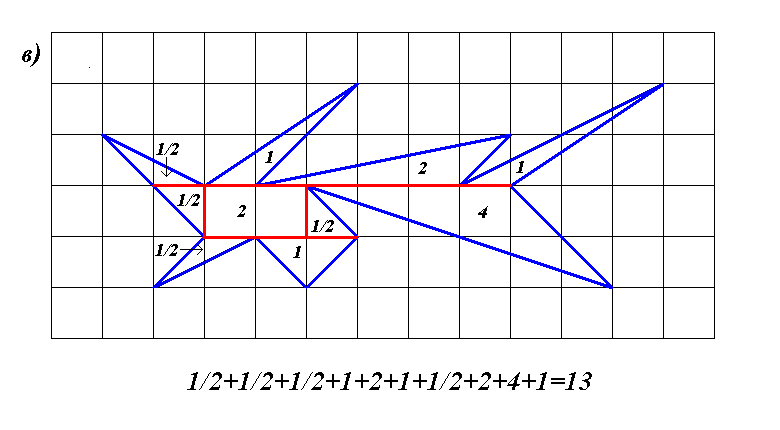
Посмотрев на то, как Олег думает над своим куском торта, Андрей задумался над тем куском, которые лежал перед ним (см. рис. а). Только он стал считать его площадь. Ему так понравилась эта задачка, что он стал рисовать разные фигуры и считать их площади. Посчитайте площади фигур на рисунках а, б и в. А вам понравилось?

Ответ Решение

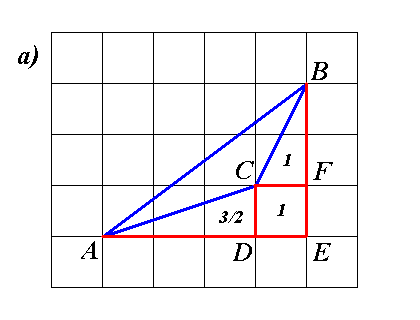
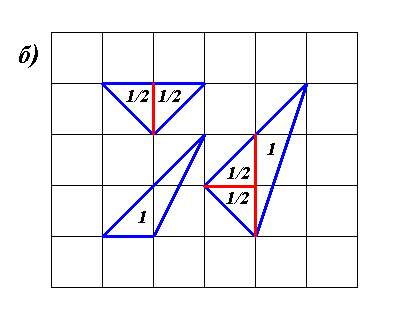
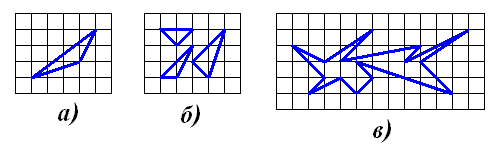Ответ. а) 2,5 клетки; б) 4 клетки; в) 13 клеток.

Решение.

Идея решения состоит в том, чтобы разбить нарисованные фигуры на части, площади которых легко вычислить. На рисунках ниже показано, как это можно сделать. Площадь прямоугольника вычисляется как произведение длин его сторон. Площадь прямоугольного треугольника равна половине площади прямоугольника, две из сторон которого являются катетами этого треугольника. А площади остальных трегольников можно вычислить как разности площадей каких-нибудь прямоугольных треугольников. Подробное решение приведем только для пункта а. На рисунках к остальным двум пунктам показано разбиение фигур на трегольники и прямоугольники и указана площадь каждого из них.

Рассмотрим треугольник ABE (см. рисунок). Он состоит из четырех частей: интересующего нас треугольника ABC, двух прямоугольных треугольников ACD и BCF и квадрата CDEF. Поэтому площадь треугольника ABE есть сумма площадей перечисленных фигур: S_ABE = S_ABC + S_ACD + S_BCF + S_CDEF, откуда находим S_ABC = S_ABE − S_ACD − S_BCF − S_CDEF = ¹/₂ · 3 · 4 − ¹/₂ · 3 · 1 − ¹/₂ · 1· 2 − 1 · 1 = 6 − 1,5 − 1 − 1 = 2,5.

7.

Юра, посмотрев на Олега с Андреем стал мерить стороны своего треугольного куска торта. Две из них оказались равны 3,8 см и 0,6 см соответственно, а про третью он всем говорил, что ее длина выражается целым числом сантиметров. Чему была равна длина третьей стороны?

Ответ Решение

Ответ. 4 см.

Решение. Неравенство треугольника состоит в том, что сумма длин любых двух его сторон больше, чем длина третьей стороны. Обозначим искомую длину стороны через l. В силу неравенства треугольника l<3,8+0,6=4,4; аналогично, 3,8<0,6+l, откуда l>3,2. Таким образом, 3,2<l<4,4. А единственное целое число, удовлетворяющее этому двойному неравнеству, есть число 4.

8.

Андрей так увлекся площадями кусков тортов, что стал делать наоборот: придумывать фигуры с какой-нибудь интересной площадью и рисовать их в конце своей тетради по геометрии. Например, он нарисовал квадраты с площадями в 2 и 5 раз больше площади одной тетрадной клетки. А вы сможете нарисовать такие квадраты?

Ответ Решение

Ответ.

Решение.

На рисунках, данных в ответе, показано, как разрезать построенные квадраты на части площадью в полклетки (п. а) или в одну клетку (п. б).

Можно найти длины сторон этих квадратов. Так как площадь квадрата равна квадрату длины его стороны, то длина стороны квадрата равна квадратному корню из площади квадрата. (По определению квадратный корень из неотрицательного числа a — это такое неотрицательное число b, что b²=a. Обозначается b=√a.) В случае а) это √2, а в случае б) √5. Точное значение этих чисел мы получить не можем, но можно построить отрезки с такими длинами.
Сделать это поможет теорема Пифагора. Она утверждает, что сумма квадратов длин катетов прямоугольного трегольника (то есть сторон, лежащих против вершин острых углов) равна квадрату длины его гипотенузы (то есть стороны, лежащей против вершины прямого угла). Значит, длина гипотенузы прямоугольного треугольника равна квадратному корню из суммы квадратов длин его катетов. Заметим, что 2 = 1² + 1², 5 = 1² + 2². Поэтому отрезки длины √2 и √5 можно построить как гипотенузы прямоугольных треугольников с катетами длин 1 и 1 или 1 и 2 соответственно. Такие треугольники несложно нарисовать на клетчатой бумаге.

9.

А Олег увлекся разрезаниями. Вот он и задумался: верно ли, что квадрат можно разрезать на любое число квадратов (не обязательно равных), начиная с 6?

Ответ Решение

Ответ. Можно.

Решение.

1. Заметим, что квадрат можно разрезать на любое четное число квадратов, начиная с 4. Как получить 2n квадратов, показано на рисунке. Вдоль двух сторон исходного квадрата разместятся по n квадратов со стороной ^a/_n (где a — сторона исходного квадрата). Всего таких маленьких квадратиков получится 2n − 1 (один из них граничит сразу с двумя сторонами исходного квадрата). Оставшаяся часть будет также квадратом, но со стороной длины a·^{(n − 1)}/_n.

2. Если уже построено разбиение исходного квадрата на 2n квадратов, то можно легко получить его разбиение на 2n + 3 квадратов. Для этого любой квадрат данного разбиения надо разделить на четыре равных квадрата. Таким образом, с учетом пункта 1 мы можем получить разбиение на любое нечетное число квадратов, начиная с 4+3=7. Теперь задача полностью решена.

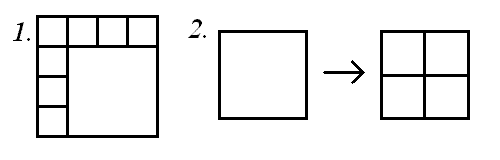
10*.

Докажите, что Олег сможет разрезать правильный треугольник на любое число правильных треугольников (не обязательно одинаковых), начиная с шести.

Решение

Решение. Решение этой задачи аналогично решению предыдущей. На рисунке показано, как разбить треугольник на четное число треугольников. Увеличить число треугольников в разбиении на 3 можно, разрезав любой из треугольников на 4 части по его средним линиям (отрезкам, соединяющим середины его сторон).

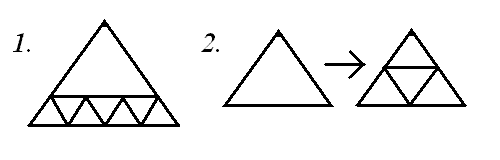
11*.

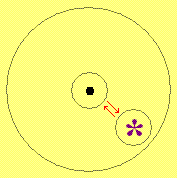
В условиях задачи №1: смогли бы девочки переместить звездочку в центр торта, разрезав верхний корж только на две части?

Ответ Решение

Ответ. Смогли бы.

Решение. Надо вырезать из верхнего коржа круглый кусок, содержащий центр коржа и звездочку, причем центр и звездочка должны быть расположены симметрично относительно центра вырезаемого куска (см. рисунок). После этого кусок нужно повернуть на 180° вокруг его собственного центра.