
МАЛЫЙ МЕХМАТ МГУ

Кружок 8 класса
Руководители Сергей Александрович Дориченко и Степан Львович Кузнецов
2007/2008 учебный год
2007/2008 учебный год
Листок 7
Если a и b — целые числа, причём b<0, то существуют такие целые числа q и r, что a=bq+r и 0≤r<b. Числа q и r определены однозначно для каждых a и b. Число r называется остатком от деления a на b.- 1.
- Ковбой Джо приобрел в салуне несколько бутылок Кока-Колы по 1 доллару 40 центов за штуку, несколько сэндвичей по 35 центов и бифштекс за 2 доллара 80 центов. Бармен сказал, что с него 20 долларов 50 центов. Ковбой Джо застрелил бармена. Докажите, что было за что.
- 2.
- Докажите, что произведение любых трех последовательных натуральных чисел делится на 6.
- 3.
- Про заданные семь чисел известно, что сумма любых шести из них делится на 5. Докажите, что каждое из чисел делится на 5.
- 4.
- Докажите, что для любого натурального n найдутся n подряд идущих составных натуральных чисел.
- 5.
- Найдите p, если: а) p, p + 10, p + 14 — простые числа; б) p, 2p + 1, 4p + 1 — простые числа.
- 6.
- Найдите остаток от деления на 7 произведения 7778×7779×7780×7781×7782×7783.
- 7.
- Стёпа играл в солдатиков. Сначала он попытался построить их парами, но один солдатик оказался лишним. Тогда Стёпа стал строить солдат тройками, но снова один остался. Та же история повторялась и при построениях по 4, по 5 и по 6. Стёпа уже приготовился выбрасывать непослушного, но тут ему наконец удалось построить всех в колонну по 7. Сколько солдат могло быть у Стёпы, если их было меньше 1000?
- 8.
- Докажите, что а) квадрат нечётного числа дает остаток 1 при делении на 8; б) квадрат целого числа либо делится на 9, либо при делении на 3 даёт остаток 1.
- 9.
- Сумма квадратов двух целых чисел делится на 9. Докажите, что каждое число делится на 3.
- 10.
-
Решите в целых числах уравнение
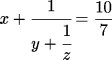
- 11.
- Докажите, что число, имеющее нечётное число делителей, является точным квадратом.
- 12.
- Даны сорок чисел, ни одно из которых не делится на 5. Докажите, что сумма их сороковых степеней делится на 5.