МАЛЫЙ МЕХМАТ МГУ

Кружок 8 класса

Занятие 1 (17 сентября 2016 года)

1.

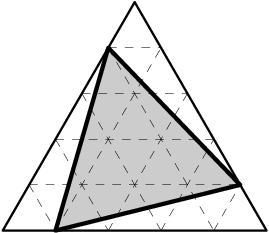
В правильный треугольник площади 25 вписан другой треугольник так, как показано на рисунке. Найдите площадь заштрихованного треугольника.

2.

Сначала на доске написано число ноль. Двое по очереди делают следующие ходы: игрок выбирает любое из чисел 1, 2, 3 или 4 и прибавляет его к записанному на доске числу. Выигрывает тот, что первым назовёт число, большее 25. Есть ли у одного из игроков выигрышная стратегия? Если есть, то как он должен играть?

3.

Существует ли пятиугольник, никакие две из пяти диагоналей которого не имеют общих точек (кроме вершин)?

4.

В квадратном ковре со стороной 10 м моль проела 80 дырок (дырки считаются точечными). Докажите, что из него можно вырезать коврик стороной 1 м, не содержащий внутри себя ни одной дырки. Дырки а) могут; б) не могут находиться на границе вырезаемого коврика.

5.

На чаепитие собрались 25 ребят. Каждый принёс по 2 пирожных. Все пирожные разложили на 25 тарелок (по 2 на тарелку). Докажите, что, как бы ни были размещены пирожные, можно так раздать тарелки ребятам, что каждому достанется хотя бы одно пирожное, которое он сам принёс.

6.

Радиоуправляемая игрушка выезжает из некоторой точки. Она движется по прямой, а по команде может поворачивать налево ровно на 17° (относительно прежнего направления движения). Какое наименьшее число команд необходимо, чтобы игрушка вновь прошла через точку старта?

7.

Имеются шесть монет различного веса. Докажите, что нельзя упорядочить их по возрастанию массы, сделав меньше десяти взвешиваний.