МАЛЫЙ МЕХМАТ МГУ

Кружок 9-11 классов

Враньё!

1.

Докажите, что 2=1.

Решение

Решение. Пусть \(a=b\neq0\). Тогда \(a^2-ab=a^2-b^2\), по формуле разности квадратов \(a(a-b)=(a+b)(a-b)\), сокращаем на \(a-b\) и получим: \(a=a+b\), отсюда \(a=2a\), сократим на a и получим искомое 1=2.

2.

Пустой стакан равен полному.

Решение

Решение. Наполовину пустой стакан равен наполовину полному. Удваиваем, получаем искомое.

3.

Для того, чтобы видеть, совсем не обязательно иметь иметь глаза.

Решение

Решение. Без правого глаза мы видим. Без левого тоже видим. А поскольку кроме левого и правого глаза других глаз у нас нет, то оказывается, что ни один глаз не является необходимым для зрения.

4.

Докажите, что 3=2.

Решение

Решение. Рассмотрим очевидное равенство: \((2 - 2{,}5)^2 = (3 - 2{,}5)^2\). Отсюда, извлекая квадратный корень, имеем: \(2 - 2{,}5 = 3 - 2{,}5\). Прибавляем к обеим частям этого равенства по 2,5. чтд

5.

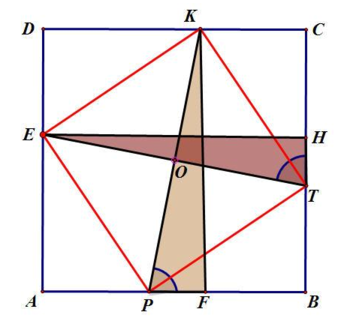
Прямоугольник, вписанный в квадрат, является квадратом.

Решение

Решение. Пусть прямоугольник EKTP вписан в квадрат ABCD. Прoведем EH⊥BC и KF⊥AB. Понятно что отрезки ЕН и KF равны между собой. KP и ET тоже равны между собой как диагонали прямоугольника. Поэтому прямоугольные треугольники ETH и KPF равны, тогда равны и углы KPF и ETH. Поэтому сумма углов OPB и OTB равна 180°. А тогда и сумма углов POT и TBP тоже равна 180°. И так как угол В прямой, то и угол POT тоже прямой. Диагонали прямоугольника пересекаются под прямым углом, значит, EKTP — квадрат.

6.

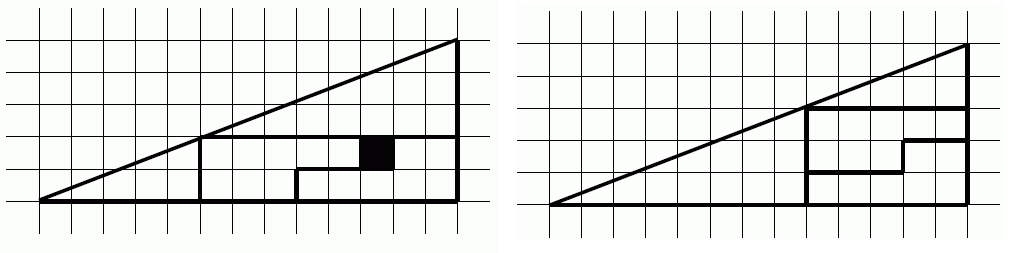
Докажите, что 65=64.

Решение

Решение. Разрежем треугольник с дыркой площади 64 на части и сложим треугольник без дырки, площади 64.

7.

Докажите Великую Теорему Ферма: при \(N>2\) уравнение \(X^N+Y^N=Z^N\) не имеет решения в натуральных числах.

Решение

Решение. Запишем теорему Пифагора таким образом: \(X^2 + Y^2 = R^2\), где \(X\), \(Y\), \(R\) — целые числа, а \(Z\) — должно быть нецелым. Попробуем доказать. Понятно, \(Z\) не равно \(R\) при одних и тех же \(X\), \(Y\). Запишем длины сторон треугольника \(XYR\) в тригонометрическом виде: \(X = R \sin A\), \(Y = R \cos A\). А значит, \(Z^N = X^N + Y^N = R^N (\sin A + \cos A)\). \(Z = R \sqrt[N]{\sin A + \cos A}\). Ранее мы доказали, что \(Z\) всегда меньше \(R\), стало быть, \(\sin A + \cos A < 1\). Такую тригонометрическую функцию можно найти в любом учебнике математики и убедиться, что если значение функции < 1, то угол \(A\) больше 60° и меньше 90°. А что будет в этом случае с прямым углом \(В\), находящимся между катетами? Он больше уже не будет прямым и окажется в тех же пределах: 60° < B < 90°. Любой десятиклассник, у которого по математике выше тройки, с ходу воспроизведет вам формулу соотношения сторон треугольника \(Z^2 = X^2 + Y^2 - 2 XY \cos B\). Рассмотрим выражение. При 60° < B < 90° cos B — число не целое. А значит, и Z является таковым при целых значениях X и Y.