
|
Избранные задачи домашней олимпиады А.В. Спивака
для 6–8 классов.
2002–2003 учебный год.
Часть IV
|
31.
| В тюрьму поместили 100 узников. Надзиратель сказал им: «Я дам вечер поговорить друг с другом, а потом рассажу по отдельным камерам, и общаться вы больше не сможете. Иногда я буду кого-то из вас отводить в комнату («красный уголок»), где есть лампа. Уходя из комнаты, вы можете оставить лампу хотите включённой, хотите — выключенной. Если в какой-то момент кто-то из вас скажет мне, что вы все уже побывали в комнате, и окажется прав, то я всех выпущу на свободу. А если он ошибётся — скормлю крокодилам. И не волнуйтесь, что кого-то забуду: если будете молчать, то вы все побываете в комнате, причём ни для кого никакое посещение комнаты не станет последним». Придумайте стратегию, гарантирующую узникам освобождение, если лампа изначально а) выключена; б) неизвестно, включена или выключена. | Указание
Решение пункта а)
Решение пункта б) |
|
Указание. Узники могут выбрать «счётчика», который делает следующее: если, придя в комнату, он обнаруживает свет включённым, то прибавляет к уже сосчитанному числу единицу и выключает свет. | |
| |
а) Решение. Как сказано в указании, узники выберут счётчика. Каждый из остальных узников действует так: если, придя в красный уголок, он обнаруживает, что свет не горит, и до этого ни разу не включал свет, то он щёлкает выключателем. Когда число у счётчика станет равно 99, счётчик заявит, что все узники уже побывали в комнате. | |
|
б) Решение. Как и в пункте а), узники выбирают счётчика. Каждый из остальных узников действует так: если, придя в красный уголок, он обнаруживает, что свет не горит, и до этого включал свет не более одного раза, то узник щёлкает выключателем. Когда число у счётчика станет равно 197, он заявит, что все узники уже побывали в красном уголке. | |
|
| |
32.
| Какое наибольшее количество брусков размером 1×2×2, не имеющих общих внутренних точек, можно расположить в кубе размером 3×3×3?
| |
33.
| Робинзон Крузо поручил Пятнице провести перепись собак, кошек, коз и попугаев. Пятница решил отмечать каждую собаку палочкой, кошку — палочкой и ноликом,
козу — двумя ноликами. Может ли Пятница отмечать каждого попугая какой-нибудь последовательностью из палочек и кружочков, чтобы по его отчёту (Пятница пишет слева направо
подряд без пробелов) Робинзон мог однозначно установить, сколько каких животных приняли участие в переписи?
| |
34.
| На столе стоят 11 блюдец, первоначально пустых. Два игрока ходят поочерёдно. Ход состоит в том, чтобы положить по одной копейке в каждое из 10 блюдец. Выигрывает тот, после чьего хода впервые в каком-то блюдце соберётся 21 копейка. Может ли игрок, положивший копейки первым, обеспечить себе выигрыш? | Ответ
Решение
| | |
|
Решение. Первый игрок первым ходом положил копейки в некоторые 10 блюдец. Второй игрок может свои первые 10 ходов делать так, чтобы в каждое из этих 10 блюдец ровно один раз копейка не добавлялась. В результате после первых 20 выкладываний (то есть после 10 ходов первого и 10 ходов второго) ни в одном из 11 блюдец число копеек не достигнет 20;
в то же время по принципу Дирихле по крайней мере в двух блюдцах окажется по 19 копеек. После 11-го хода первого игрока хотя бы в одном блюдце окажется 20 копеек; добавив туда 21-ю копейку, второй игрок выиграет. | |
|
| |
35. | Точка M — середина основания BC равнобедренного треугольника ABC. На боковых сторонах AB и AC
отмечены точки U и V соответственно так, что AU не равно AV и MU = MV. Докажите, что величина угла UMV вдвое больше величины угла АBС.
| |
36.
| На плоскости нарисовали три окружности, разбивающие плоскость на 8 частей. В каждую из семи ограниченных частей написали число 1. За одну операцию разрешено сменить внутри любой из окружностей все знаки на противоположные или (опять-таки внутри некоторой окружности) возвести числа в квадрат. Можно ли за несколько таких операций добиться ситуации, когда в области, являющейся пересечением всех трёх кругов, будет число –1, а в остальных шести ограниченных областях будут единицы?
| |
37.
| На полосу положили квадрат, сторона которого равна ширине полосы. Граница квадрата пересекла границу полосы в четырёх точках. Докажите, что прямые, проходящие накрест через эти точки, пересекаются под углом 45°.
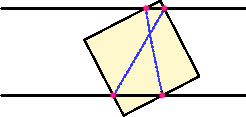
| Указание |
Указание. Передвиньте квадрат параллельно одной из его сторон так, чтобы одна из вершин оказалась на границе полосы. Проведя из этой вершины высоту полосы, рассмотрите возникшие пары равных
треугольников. | |
|
| |
38.
| Выпишите первые двадцать натуральных чисел в таком порядке, чтобы никакая сумма нескольких подряд написанных чисел не делилась на 20. (Достаточно одного способа.) | Ответ | Ответ. 1, 20, 2, 19, 3, 18, 4, 17, 5, 16, 6, 15, 7, 14, 8, 13, 9, 12, 10, 11. | |
|
| |
39.
| На доске были написаны 10 последовательных натуральных чисел. Когда стёрли одно из них, то сумма девяти оставшихся оказалась равна 2002. Какие числа остались на доске? | Ответ
Решение |
Ответ. 218, 219, 220, 221, 222, 224, 225, 226 и 227. | |
| Решение. Обозначим наименьшее из чисел буквой x. Тогда
x + (x + 1) + (x + 2) + (x + 3) + (x + 4) + (x + 5) + (x + 6) + (x + 7) + (x + 8) + (x + 9) – (x + y) = 2002,
где x + y — вычеркнутое число (так что 0 ≤ y ≤ 9). Упростим уравнение:
10x + 45 – x – y = 2002,
то есть
9 x = 1957 + y.
Поскольку число 1957 при делении на 9 даёт остаток 4, то y = 5. Значит, x = 1962 : 9 = 218. | |
|
| |
40.
| В телеконкурсе участвовали 8 юношей и 8 девушек. Каждый юноша поссорился с 14 участниками передачи, а каждая девушка — с 7 участниками. (Ссоры взаимные.) Докажите, что из участников передачи можно сформировать 8 пар, каждая из которых состоит из не поссорившихся между собой девушки и юноши. | Решение | Решение. Поскольку каждый юноша не поссорился не более чем с одной девушкой и поскольку каждая девушка хотя бы с одним юношей не поссорилась, то на самом деле для каждого юноши есть единственная девушка, с которой он не поссорился. (А девушки между собой вообще не ссорились, хотя это не наше дело.) | |
|
|
|


