МАЛЫЙ МЕХМАТ МГУ

Кружок 9-11 классов

Ликвидация безграмотности!

Комбинаторика. 16 октября 2010 года

Великое напоминание: Через 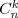обозначается количество способов выбрать из множества, содержащем n элементов, подмножество, содержащее k элементов. Или, по-простецки, количество способов выбрать из n предметов k без учета порядка.

1.

Вспомните комбинаторные доказательства следующих тождеств:

a)

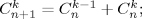
b)

c)

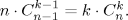
2.

Докажите комбинаторно, что

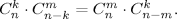
Еще одно великое напоминание: (бином Ньютона)

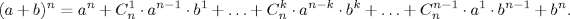
3.

Вспомните доказательства через бином Ньютона следующих тождеств:

a)

b)

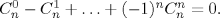
4.

Сколько существует способов добраться из легого нижнего до правого верхнего угла в прямоугольнике n×k, если за каждый ход можно идти только вверх или вправо?

Указание

Указание. А когда мы можем сходить наверх?

5.

Для проведения вступительной олимпиады преподаватели разбивают 65 школьников следующим образом: список в алфавитном порядке разбивается на 4 части, первая идет в первую аудиторию, вторая — во вторую и т.д. При этом в каждую аудиторию отправляется хотя бы один школьник. Сколькими способами можно произвести распределение?

Указание

Указание. По сути разбить список значит провести три черты где-то между детьми.

6.

В ряд стоят пять ящиков. Сколькими способами можно разложить по этим ящикам одиннадцать одинаковых шаров так, чтобы ни один ящик не оказался пустым?

7.

В ряд стоят шесть ящиков. Сколькими способами можно разложить по этим ящикам десять одинаковых шаров, если разрешается, чтобы ящики оставались пустыми?

8.

Сколькими способами можно разрезать ожерелье, состоящее из 30 различных бусин, на 8 частей (резать можно только между бусинами)?

9.

Сколько есть способов переплести 12 одинаковых книг в красные, зеленые или синие переплеты, если a) обязательно; b) не обязательно использовать все цвета?

10*

У нефтяной компании есть n цистерн. Сколькими способами можно составить k составов для отправки буржуям

a)

с учетом порядка, при том, что состав может быть пустым?

b)

каждый состав должен быть непуст?

с)

составы без учета порядка и могут быть пустыми?
Составы считаются различными, поэтому обмен двух составов местами считается новым вариантом.