МАЛЫЙ МЕХМАТ МГУ

Кружок 7 класса

Листок 8.

1.

Двое часов начали бить одновременно. Первые бьют через каждые 2 с, вторые - через каждые 3 с. Одновременные удары сливаются и воспринимаются как один. Сколько времени пройдёт между первым и тринадцатым ударами? (Всё это время бьют и те и другие часы).

2.

Как, имея лишь два сосуда ёмкостью 3 л и 5 л, набрать (в один из них) из крана 4 л воды?

3.

Сколькими способами из чисел
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15
можно выбрать два числа так, чтобы они не были соседями?

4.

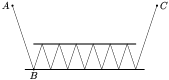Два зеркала расположены
горизонтально одно над
другим. Луч света
выпустили из точки A
в точку B. Отражаясь
от зеркал по закону "угол падения равен углу отражения", луч попал в точку C (смотрите рисунок). Попадёт ли луч в точку C, если увеличить расстояние между зеркалами вдвое, подняв верхнее зеркало? Если да, то как изменится длина пути света (от A до C)?

5.

а)

Сколько можно написать разных 10-значных чисел, используя только цифры 1 и 2?

б)

На дереве растут 10 разных яблок. Сколькими способами можно выбрать несколько из них?

6.

Боб и Джо играют на листке размером

а)

7×7 клеток;

б)

8×8 клеток. Ходят по-очереди, начинает Боб. За ход игрок ставит крестик в любую клетку, если в ней и в соседних (по стороне) клетках нет крестика. Проигрывает тот, кому некуда ходить. Кто из ребят может всегда выигрывать?

7.

Торговец принёс на рынок мешок орехов. Первый покупатель купил 1 орех, второй - 2 ореха, третий - 4, и так далее: каждый следующий покупатель покупал вдвое больше орехов, чем предыдущий. Орехи, купленные последним, весили 50 кг, после чего у торговца остался один орех. Сколько килограммов орехов было у торговца вначале? (Все орехи одинаковые.)

8.

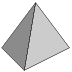
а)

Фабрика игрушек выпускает
разноцветные треугольные
пирамидки (одного размера).
У каждой пирамидки 4
равносторонних грани: желтая, красная, синяя и зелёная. Сколько разных видов пирамидок может выпускать эта фабрика?

б)

Тот же вопрос, если фабрика выпускает кубики (одного размера) с желтой, красной, синей, зелёной, белой и чёрной гранями.

Дополнительные задачи

9.

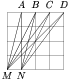Найдите сумму углов
MAN + MBN + MCN + MDN
(смотрите рисунок).

10.

В левом нижнем углу шахматной
доски 8×8 стоит король. Петя и Вася по очереди передвигают короля либо вверх, либо вправо, либо вправо-вверх (по диагонали) на одну клетку. Проигрывает тот, кто не может сделать ход. Начинает Петя. Кто из ребят может обеспечить себе победу и как ему играть?

11.

На полке стоят 5 книг.
Сколькими способами их
можно переставить
(в другом порядке) так,
чтобы ни одна книга
не осталась на месте?