МАЛЫЙ МЕХМАТ МГУ

Кружок 9-11 классов

Рекуррентные соотношения

19 февраля 2011 года

Научимся решать рекуррентные линейные соотношения второго порядка. То есть писать явные формулы для рекуррентно заданной последовательности.

1.

Выведите формулу общего члена и суммы первых n членов следующих последовательностей:

a)

(арифметическая прогрессия) x_n+1 = x_n + a;

b)

(геометрическая прогрессия) x_n+1 = a · x_n.

2.

Выведите формулу общего члена и суммы первых n членов следующей рекуррентной последовательности x_n+1 = a · x_n + b (такая последовательность называется арифметико-геометрической).

3.

Рассмотрим последовательность {r_n}, удовлетворяющую соотношению r_n+2 = 5 · r_n+1 − 6 · r_n (назовем это соотношение (1)).

a)

Докажите, что для любого числа α последовательность {α·r_n} также удовлетворяет этому соотношению;

b)

Докажите, что если две последовательности {r_n} и {s_n} удовлетворяют (1), то и последовательность {r_n + s_n} ему также удовлетворяет;

c)

Найдите геометрическую прогрессию, удовлетворяющую соотношению (1). Сколько различных таких прогрессий?

d)

Используя результаты предыдущих пунктов этой задачи, напишите формулу с двумя произвольными параметрами c₁ и c₂, являющуюся формулой n-го члена для последовательностей, удовлетворяющих (1);

e)

Докажите, что ваша формула исчерпывает все последовательности, удовлетворяющие (1) (обратите внимание, что каждая такая последовательность однозначно задается своими двумя первыми членами).

4.

Проделайте аналогичные операции и найдите формулу n-го члена последовательности Фибоначчи: F₁ = F₂ = 1, F_n+2 = F_n+1 + x_n.

5.

Полученная явная формула для чисел Фибоначчи называется формулой Бине. Не верится, что она задает целочисленную последовательность, но это так. Впрочем, если вспомнить про бином Ньютона, то это становится очевидным. Докажите целочисленность этой формулы при каждом натуральном n через бином Ньютона.

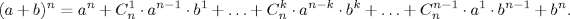
6.

На первой клетке полоски 1×n стоит шашка. За один ход разрешается передвинуть шашку вправо на одну или две клетки. Обозначим через f_n число различных способов переместить шашку из первой клетки в n-ую. Найдите реккурентную зависимость f_n от f_{n − 1} и f_{n − 2}.

7.

Найдите сумму n чисел 1 + 11 + 111 + ... + 11...11.

8.

Сколькими способами можно разбить число N на слагаемые, каждое из которых равно одному из натуральных чисел 1, 2, 3, ..., n? Порядок слагаемых не важен.

26 февраля 2011 года

8.

Последовательность {a_n}, состоящая из натуральных чисел, такова, что a₁ > a₀ и a_n+1 = 3·a_n − 2·a_n−1. Докажите, что a₁₀₀ ≥ 2¹⁰⁰.

9.

Дана последовательность {x_n}. Известно, что x₁ = x₂₀₁₀ = 2010 и x_n = −x_n−1 + 2·x_n−2. Докажите, что x_n = 2010 для всякого n.

10.

Найдите количество способов раскрасить полоску 1×n в три цвета: красный, синий и зеленый — так, что за красным цветом не следует зеленый (но при этом может ему предшествовать).