
МАЛЫЙ МЕХМАТ МГУ

Кружок 6 класса
Руководитель Дмитрий Александрович Коробицын
2011/2012 учебный год
2011/2012 учебный год
Занятие 8 (12.11.2011). Длины и расстояния
- 1.
-
Отрезок, равный 28 см, разделён на три (возможно неравных) отрезка.
Расстояние между серединами крайних отрезков равно 16 см. Найдите
длину среднего отрезка.
Ответ. 4 см.Решение. Заметим, что сумма половин двух крайних отрезков равна 28 − 16 = 12 см, значит, сумма их длин равна 2·12 = 24 см, но тогда длина среднего отрезка равна 28 − 24 = 4 см.
- 2.
-
На стороне AC треугольника ABC отметили точку E. Известно, что
периметр треугольника ABC равен 25 см, треугольника ABE — 15
см, треугольника BCE — 17 см. Найдите длину отрезка BE.
Ответ. 3.5 см.Решение. Сложим периметры треугольников ABE и BCE. С одной стороны, мы получим сумму периметра треугольника ABC и удвоенного отрезка BE, с другой — 32 см. Откуда следует, что 2BE = 32 − 25 = 7 см, и BE = 3.5 см.
- 3.
-
Длина стороны AC треугольника ABC равна 3.8 см, длина стороны
AB — 0.6 см. Известно, что длина BC — целое число. Чему
она может быть равна?
Ответ. 4 см.Решение. Известно, что в треугольнике любая сторона меньше суммы двух других. Поэтому сторона BC меньше AB + AC = 3.8 + 0.6 = 4.4 см. Также BC + AC > AB, т.е. BC + 0.6 > 3.8, BC > 3.2 см. Получили что BC, длина которой целая, удовлетворяет неравенствам 4.4 > BC > 3.2, т.е. BC = 4 см.
- 4.
-
Прямоугольник разбит на 9 меньших прямоугольников. Периметры
четырёх из них указаны на рисунке. Найдите периметр
прямоугольника x.
10 x 11 12 13 Ответ. 11.Решение 1. (С использованием прямоугольника с периметром 11.) Посмотрим на прямоугольники с периметром 11 и 12. Горизонтальные стороны у них равны, а сумма двух вертикальных сторон нижнего на 1 больше вертикальных сторон верхнего. Это означает, что в последнем столбце, у среднего прямоугольника периметр на 1 меньше, чем у прямоугольника с периметром 13, т.е. 12. Применяя аналогичные рассуждения для прямоугольников с периметрами 10 и 11, получим, что у x периметр равен 12 − 1 = 11.Решение 2. (Без использования прямоугольника с периметром 11.) Заметим, что суммы периметров маленьких прямоугольников, стоящих в противополжных углах, равны. Тогда12 + x = 10 + 13 = 23,откуда x = 11. - 5.
-
Квадрат ABCD со стороной 2 и квадрат DEFK со стороной 1 стоят
рядом на верхней стороне AK квадрата AKLM со стороной 3.
Между парами точек A и E, B и F, C и K, D и L
натянуты паутинки. Паук поднимается снизу вверх по маршруту AEFB и
спускается по маршруту CKDL. Какой маршрут короче?
Ответ. Никакой, маршруты равны.Решение. Заметим, что в обоих маршрутах есть отрезок длины 1 (в первом это отрезок EF, во втором — KD). Теперь нарисуем сетку так, чтобы все точки из условия оказались в узлах, а стороны квадратов были параллельны линиями сетки. Теперь можно заметить, что отрезки AE и CK равны, а также отрезки BF и DL равны. Получили, что оба маршрута равны.
- 6.
-
Один прямоугольник расположен внутри другого. Может ли так быть, что
периметр внутреннего прямоугольника больше периметра внешнего?
Ответ. Нет, не может.Решение. Назовем внутренний прямоугольник маленьким, а внешний большим.
Ясно, что если стороны маленького прямоугольника параллельны сторнам большого, то каждая сторона большого больше соотвествующей стороны маленького, а, стало быть, периметр большого больше.
Разберем случай, когда стороны маленького не параллельны сторонам большого. Опишем около маленького прямоугольника средний прямоугольник так, чтобы стороны среднего были параллельны сторонам большого и вершины маленького лежали на сторонах среднего (см. рис.)
Покажем, что периметр маленького прямоугольника меньше, чем периметр среднего. Действительно, поскольку кратчайший путь между точками — отрезок, то каждая красная сторона меньше суммы двух черных отрезков, образующих с ней треугольник. Сумма всех таких черных отрезков равна периметру среднего прямогуольника. А то, что периметр среднего меньше периметра большого, мы доказали в первом случае. Значит, такого быть не могло.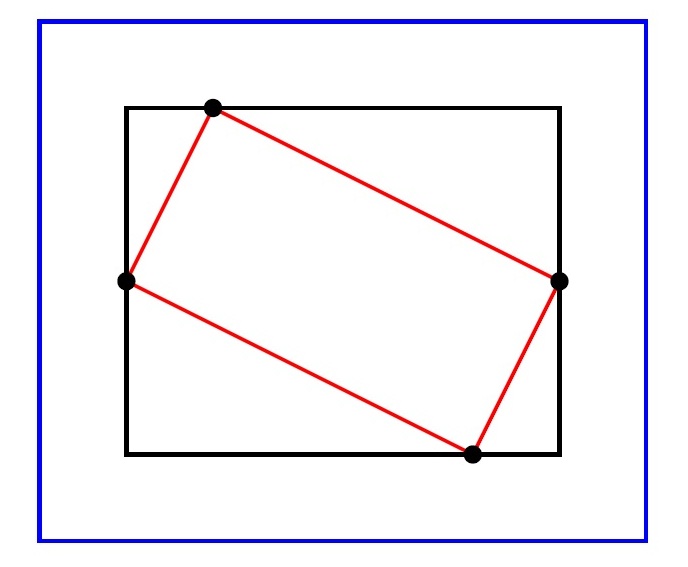
- 7.
-
На клетчатой бумаге нарисован квадрат со стороной 5. Можно ли его
разрезать на пять частей одинаковой площади, проводя разрезы только
по линиям сетки так, чтобы суммарная длина разрезов была не больше
16?
Ответ. Да, можно.Решение. Приведем пример.
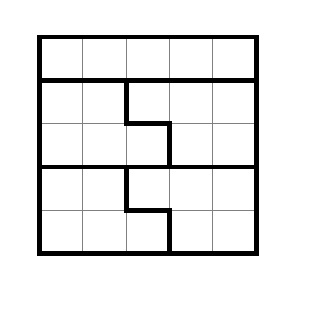
- 8.
-
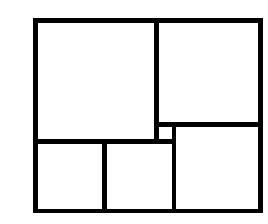 Прямоугольник составлен из шести квадратов (см. рисунок). Найдите
сторону самого большого квадрата, если сторона самого маленького
равна 1.
Прямоугольник составлен из шести квадратов (см. рисунок). Найдите
сторону самого большого квадрата, если сторона самого маленького
равна 1.
Ответ. 7.Решение. Обозначим сторону квадрата, расположенного в левом нижнем углу за x. Тогда стороны других квадратов легко вычислить. Получится, как на рисунке.Поскольку вертикальные стороны прямоугольника равны, то (2x − 1) + x = (x + 2) + (x + 1), т.е. 3x − 1 = 2x + 3, откуда x = 4. Значит, сторона самого большого квадрата равна 2·4 − 1 = 8 − 1 = 7.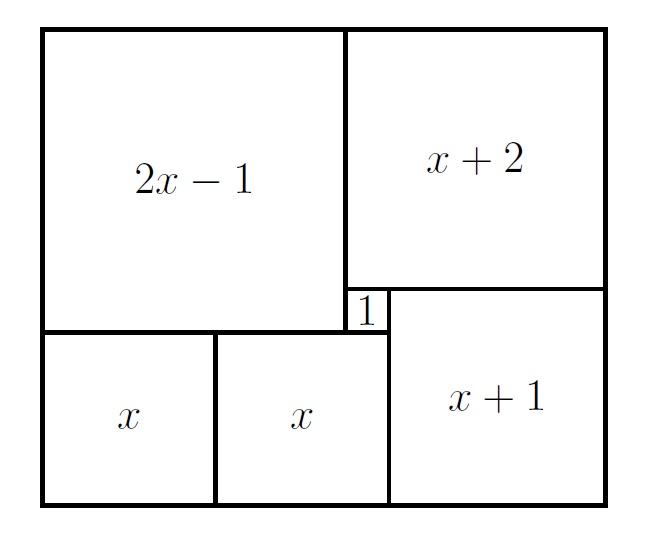
| Вы видите ошибку? Выделите её и нажмите Ctrl+Enter! |
|
|
|