МАЛЫЙ МЕХМАТ МГУ

Кружок 6 класса

Занятие 7 (05.11.2011). Математическая регата

1 тур (10 минут)

1.

Петя пообещал маме, что прочитает ещё только 50 страниц комиксов и будет учить математику. Прочтя 50-ю, 51-ю, 52-ю, ..., 100-ю страницу, Петя честно принялся за уроки, однако мама всё равно упрекнула его за несдержанное слово. Права ли мама?

Решение

Решение. Права, потому что Петя на самом деле прочитал 51 страницу.

2.

Из спичек выложено равенство XIV − XVI = II. Переместите одну спичку так, чтобы равенство стало верным.

Решение

Решение. Можно переложить одну спичку от знака равенства к минусу. Получим XIV = XVI − II.

3.

Цифры трёхзначного числа записали в обратном порядке. Может ли так быть, что сумма этих двух чисел записывается только нечётными цифрами.

Решение

Решение. Может. 734 + 437 = 1171.

2 тур (15 минут)

1.

Сундук, полный золота, весит 32 пуда, а сундук, заполненный золотом наполовину, — 17 пудов. Сколько весит пустой сундук?

Решение Ответ

Решение. 32 − 17 = 15 — вес половины золота.
Тогда всё золото весит 15·2 = 30 пудов. Значит, вес сундука 32 − 30 = 2 пуда.

Ответ. 2 пуда.

2.

Разрежьте фигуру, изображённую на рисунке, на четыре равные части.

Решение

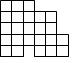Решение. Например, так:

3.

Кузнечик прыгает по прямой, причём в первый раз он прыгнул на 1 м в какую-то сторону, во второй раз — на 2 м в какую-то сторону, в третий раз — на 3 м и так далее. Докажите, что через 50 прыжков он не сможет оказаться там, где начинал.

Решение

Решение. Раскрасим точки, находящиеся на расстоянии от начального расположения кузнечика, равном целому числу метров, поочерёдно в чёрный и белый цвет. Тогда прыжок нечётной длины меняет цвет точки, в которой находится кузнечик, а ход чётной длины не меняет. Ходов нечётной длины было 25, значит и цвет менялся 25 раз, поэтому в конце он отличается от начального. А значит, там, где начинал, кузнечик оказаться не может.

3 тур (15 минут)

1.

В компьютерной программе Excel столбцы таблиц нумеруются латинскими буквами. Первые 26 столбцов занумерованы от A до Z, 27-й столбец обозначен AA, 28-й — AB и т.д. Как занумерован 700-й столбец?

Решение Ответ

Решение. 700 = 26·26 + 24, поэтому цикл вторых букв от A до Z повторится 26 раз. Поскольку в обозначении первых 26 столбцов первая буква не писалась, то последний 26-й цикл будет соответствовать букве Y. Осталось ещё 24 столбца. Первая буква в их обозначении будет Z, а вторые буквы будут от A до X.

Ответ. ZX.

2.

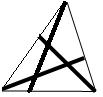Большой треугольник разбит тремя жирными отрезками на четыре треугольника и три четырёхугольника. Сумма периметров четырёхугольников равна 25 см. Сумма периметров четырёх треугольников равна 20 см. Периметр исходного большого треугольника равен 19 см. Найдите сумму длин жирных отрезков.

Решение Ответ

Решение. Рассмотрим сумму периметров всех частей. Длины всех жирных отрезков будут посчитаны по 2 раза, а длины сторон исходного треугольника по 1 разу. То есть, чтобы получить сумму длин жирных отрезков нужно вычесть из полученной суммы периметр исходного треугольника и разделить на 2. Итого получаем (25 + 20 − 19)⁄2 = 13.

Ответ. 13 см.

3.

Четыре друга участвовали в олимпиаде. Витя решил больше всех задач — восемь, а Петя меньше всех — пять. Каждая задача олимпиады была решена ровно тремя из друзей. Сколько задач было на олимпиаде?

Решение Ответ

Решение. Так как каждая задача была решена ровно тремя из друзей, то количество полученных от них решений делится на три (т.е. если сложить количества решённых каждым задач, то получится число, делящееся на три). Так как самое маленькое количество решённых задач — 5, а самое большое — 8, то оставшиеся два числа либо 6 и 6, либо 6 и 7, либо 7 и 7. Тогда сумма может быть равна 25, 26 или 27. На три делится только 27. Количество задач в три раза меньше числа решений, поэтому равно 9.

Ответ. 9 задач.

4 тур (20 минут)

1.

Найдите такие четыре различные несократимые дроби, что знаменатель каждой из них больше 20, а знаменатель любой суммы двух, трёх или четырёх этих дробей после сокращения становится меньше 20.

Решение

Решение. Например, подходят дроби ¹/₂₄, ⁷/₂₄, ¹³/₂₄, ¹⁹/₂₄.

2.

Квадрат разрезали на 8 квадратиков. Верно ли, что семь из них обязательно равны?

Решение

Решение. Нет, необязательно.

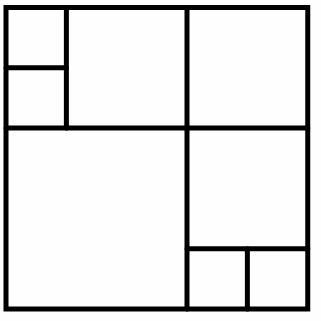
3.

На острове Невезения собрались рыцари, которые всегда говорят правду, и лжецы, которые всегда лгут, причем как рыцарей, так и лжецов было не меньше, чем по двое. Каждый присутствующий указал на каждого из оставшихся и произнес: «Ты — рыцарь!» или «Ты — лжец!«. Высказываний «Ты — лжец!» было ровно 70. Сколько было высказываний «Ты — рыцарь!«?

Решение Ответ

Решение. Заметим, что «Ты — лжец!» говорит лжец рыцарю или рыцарь лжецу, а «Ты — рыцарь!» — рыцарь рыцарю или лжец лжецу. Пусть среди собравшихся a рыцарей и b лжецов. Тогда фраза «Ты — лжец!» была сказана 2ab раз. Отсюда ab = 35. Поскольку каждое из чисел a и b не меньше 2, одно из них равно 5, а другое — 7. Поэтому фраза «Ты — рыцарь!» была сказана 5·4 + 7·6 = 20 + 42 = 62 раза.

Ответ. 62.