МАЛЫЙ МЕХМАТ МГУ

Кружок 6 класса

Занятие 23 (17.03.2012). Чётность и графы

Напомним, что граф} — это набор точек, некоторые из которых соединены линиями. Точки называются вершинами графа, линии — рёбрами.

1.

Получите из левой картинки правую, проводя линии между точками (по одной). Около каждой точки подписывайте, сколько из неё выходит линий. Как изменяются числа после каждого дорисовывания линии?

Решение

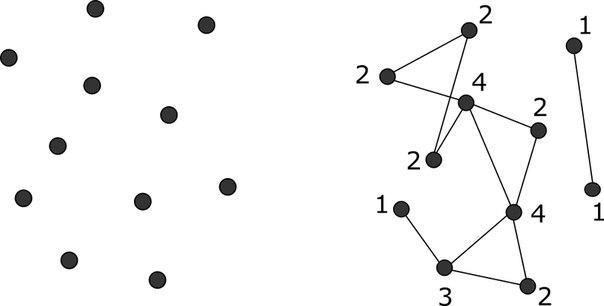Решение. После каждого дорисовывания степени двух вершин увеличиваются на 1. Вершину графа будем называть чётной, если из неё выходит чётное число рёбер, нечётной — если выходит нечётное число рёбер.

2.

а)

Как связаны числа из задачи 1 и количество рёбер в графе?

Ответ

Ответ. Сумма всех чисел равна удвоенному числу ребер, так как каждое ребро увеличивает степень ровно двух вершин на 1.

б)

Докажите, что в любом графе количество нечётных вершин чётно.

Ответ

Ответ. Поскольку сумма степеней всех вершин чётна, то и число нечётных вершин чётно.

3.

Можно ли 15 телефонов соединить проводами так, чтобы каждый был соединён ровно с 5 другими?

Ответ Решение

Ответ. Нет, нельзя.

Решение. Рассмотрим граф, в котором телефоны — это вершины. Вершины будем соединять ребром, если телефоны соединены проводом. В любом графе число нечетных вершин четно. Значит, так соединить телефоны не получится.

4.

В классе 30 человек. Может ли быть так, что у 9 из них по 3 друга в классе, у 11 — по 4 друга и у 10 — по 5 друзей?

Ответ Решение

Ответ. Нет, не может.

Решение. Посчитаем число нечетных вершин в этом графе. Их 9 + 10 = 19 — нечетное число. Значит, такого не может быть.

5.

Может ли в государстве, в котором из каждого города выходит 3 дороги, быть ровно 100 дорог?

Ответ Решение

Ответ. Нет, не может.

Решение. Пусть в графе a городов. Тогда a·3⁄2 = 100, но тогда 3a = 200, чего не может быть, так как 200 не делится на 3.

6.

Можно ли нарисовать на плоскости 9 отрезков так, чтобы каждый пересекался ровно с тремя другими?

Ответ Решение

Ответ. Нет, нельзя.

Решение. Рассмотрим граф, вершины которого соответствуют отрезку. Вершины будем соединять ребром, если соответсвующие отрезки пересекаются. Тогда получим, граф в котором нечетное число нечетных вершин. Значит, так нарисовать отрезки не получится.

7.

В некотором государстве 99 городов, некоторые пары городов соединены дорогами длиной в 1, 3 или 5 вёрст, причём от каждого города до каждого по этим дорогам можно добраться ровно одним способом. Из каждого города в каждый другой отправились гонцы с важным донесением. Докажите, что суммарное расстояние, пройденное гонцами, делится на 4.

Решение

Решение. Рассмотрим произвольную дорогу N. Эта дорога делит все города на две группы так, что из города одной группы нельзя проехать в город другой группы, не проезжая через N. Пусть в одной группе a городов, тогда в другой 99 − a. Но тогда по этой дороге проехали всего 2· a·(99 − a) раз. Т.к. a и 99 − a разной четности, то 2· a·(99 − a) делится на 4. Значит, и вся сумма делится на 4.

8.

На Малом Мехмате дети договорились послать друг другу электронные письма. Те из них, у кого число знакомых чётно, отправят письма всем знакомым, а те, у кого число знакомых нечётно, отправят письма всем незнакомым. Придя домой и включив компьютер, Гоша увидел, что ему пришло 99 писем. Докажите, что он получит ещё хотя бы одно.

Решение

Решение. Будем называть ребёнка чётным, если у него четное число знакомых, и нечётным в противном случае. Заметим, что число нечётных детей чётно. Посмотрим, от кого Гоша мог получить письма. Либо от четных знакомых, либо от нечетных незнакомых. Разберем два случая.
1) Гоша — чётный. Тогда он получит чётное число писем от знакомых и еще чётное число от незнакомых.
2) Гоша — нечётный. Тогда он получит нечётное число писем от незнакомых и еще нечётное число писем от знакомых.
В обоих случаях получили, что Гоша получит чётное число писем. Т.е. еще хотя бы одно.