МАЛЫЙ МЕХМАТ МГУ

Кружок 6 класса

Занятие 20 (25.02.2012). Примеры и контпримеры

1.

Приведите контрпример к каждому из следующих утверждений.

а)

Все простые числа — нечетные.

б)

Все прямоугольники являются квадратами.

в)

Каждое натуральное число либо простое, либо составное.

г)

Все четырехугольники, у которых все стороны равны, являются квадратами.

Ответ

Ответ. а) 2; б) прямоугольник со сторонами 1 и 2; в) 1; г) ромб, не являющийся квадратом.

2.

Вася думает, что если площадь первого прямоугольника больше площади второго, а также периметр первого больше периметра второго, то из первого можно вырезать второй. Прав ли он?

Ответ Решение

Ответ. Нет, не прав.

Решение. Из прямоугольника 1×100 нельзя вырезать квадрат 2×2.

3.

Гриб называется плохим, если в нем не менее 10 червей. В лукошке 90 плохих и 10 хороших грибов. Могут ли все грибы стать хорошими после того, как некоторые черви переползут из плохих грибов в хорошие?

Ответ Решение

Ответ. Могут.

Решение. Пусть в каждом плохом грибе ровно 10 червей, а в хорошем червей нет. Далее, пусть из каждого плохого гриба по одному червю переползут в хорошие, по 9 в каждый. В результате в каждом грибе окажется по 9 червей, и все грибы будут хорошими.

4.

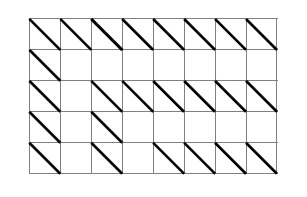
Выберите 24 клетки в прямоугольнике 5×8 и проведите в каждой выбранной клетке одну из диагоналей так, чтобы никакие две проведенные диагонали не имели общих концов.

Решение

Решение.

5.

Барон Мюнхгаузен утверждает, что может для некоторого N так переставить числа 1, 2, ..., N в другом порядке и затем выписать их все подряд без пробелов, что в результате получится многозначное число-палиндром (оно читается одинаково слева направо и справа налево). Не хвастает ли барон?

Ответ Решение

Ответ. Нет, не хвастает.

Решение. Числа можно выписать, например, так

9.18.7.16.5.14.3.12.1.10.11.2.13.4.15.6.17.8.19

Объясним, почему нужно искать пример для N ≥ 19. В палиндроме количество всех цифр, кроме, быть может, одной, должно быть четным. Однако если N = 2, ..., 9, то цифры 1 и 2 встречаются в записи чисел 1, 2, ..., N по одному разу, а если N = 10, ..., 18, то по 1 разу встречаются цифры 0 и 9.

6.

На доске написаны три различных числа от 1 до 9. Одним ходом разрешается либо прибавить к одному из чисел 1, либо вычесть из всех чисел по 1. Верно ли, что всегда можно добиться того, чтобы на доске остались только нули, сделав не более 23 ходов?

Ответ Решение

Ответ. Неверно.

Решение. Пусть вначале на доске написаны числа 1, 2 и 9, и через несколько ходов из них получились нули. Если из 9 в результате получился ноль, то вычитание производилось хотя бы девять раз. Значит, и из остальных чисел вычиталось хотя бы по девять единиц; значит, к 1 надо было сделать не меньше восьми прибавлений, а к двойке не меньше семи. Итоговое количество ходов, таким образом, не меньше 9 + 8 + 7 = 24.

7.

Рома придумал теорему: Если число A является квадратом натурального числа B, а также каждая цифра числа A делится на 3, то и каждая цифра числа B делится на 3. Верна ли ромина теорема?

Ответ Решение

Ответ. Неверна.

Решение. Например, для B=264,813. 264²=69696, 813²=660969.