Кружок для старшеклассников, не участвовавших ранее в математических кружках

Занятие 21 (28 марта 2015 года). Двойка, её оттенки и степени

1.

На какую цифру оканчивается 2¹⁰⁰?

2.

Найдите остаток от деления 2¹⁰⁰ на 3.

3.

Что больше и на сколько: 2¹⁰⁰ или 1 + 2 + 4 + 8 + ... + 2⁹⁹?

4.

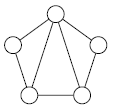Впишите в пять кружков натуральные числа так, чтобы выполнялись два условия:

• если два кружка соединены линией, то стоящие в них числа должны отличаться ровно в два или ровно в четыре раза;
• если два кружка не соединены линией, то отношение стоящих в них чисел не должно быть равно ни 2, ни 4.

5.

На столе стоят восемь стаканов с водой. Разрешается взять любые два стакана и уравнять в них количества воды, перелив часть воды из одного стакана в другой. Докажите, что с помощью таких операций можно добиться того, чтобы во всех стаканах было поровну воды.

6.

Числа 2, 4, 8, 16, 32, 64, 128, 256 и 512 расставьте в клетках таблицы 3×3 так, чтобы произведения по всем вертикалям, горизонталям и обеим главным диагоналям были равны.

7.

Обезьяна хочет узнать, из окна какого самого низкого этажа 15-этажного дома нужно бросить кокосовый орех, чтобы он разбился. У неё есть 2 ореха. Какого наименьшего числа бросков ей заведомо хватит? (Возможно, и при падении с 15-го этажа орех не разбивается. Неразбившийся орех можно бросать снова.)

8.

Сначала на экране калькулятора появилось число 1. Раз в секунду калькулятор находит какое-нибудь целое неотрицательное k такое, что число на экране делится на 2^k, и меняет число на экране, прибавляя к нему любое число от 1 до (k + 1). Незнайка полагает, что любая степень двойки рано или поздно появится на экране. Прав ли Незнайка?

9.

Разрежьте по клеточкам квадрат 7×7 на девять прямоугольников (не обязательно различных), из которых можно будет сложить любой прямоугольник со сторонами, не превосходящими 7.

10.

Докажите, что для любого натурального n существует n-значное число, кратное 2ⁿ, составленное из единиц и двоек (например, 112 кратно 2³, 2112 кратно 2⁴).