Кружок 8 класса

Занятие 11 (26.11.2011). Принцип крайнего

1.

Можно ли отметить на плоскости 100 точек так, чтобы любая из отмеченных точек лежала в середине отрезка, соединяющего две другие отмеченные точки? А в пространстве?

2.

Сумма положительных чисел x₁, x₂, ..., x₁₀₀ равна 1. Докажите неравенство x₁x₂ + x₂x₃ + ... + x₉₉x₁₀₀ ≤ ¹/₄.

3.

Докажите, что не существует выпуклого многогранника, все грани которого имеют различное количество сторон.

4.

На плоскости проведены 100 прямых. Никакие две из них не параллельны, никакие три не проходят через одну точку. На сколько частей прямые делят плоскость?

5.

На столе лежат несколько одинаковых монет без наложений. Докажите, что найдётся монета, которая касается не более трёх других.

5'.

Про 21 число известно, что сумма любых пяти из них положительна. Докажите, что сумма всех чисел положительна.

6.

По окружности расположены 6 чисел, при этом каждое число равно модулю разности двух следующих за ним по часовой стрелке. Сумма всех чисел равна единице. Найдите эти числа.

7.

Али-Баба пытается проникнуть в пещеру. У входа стоит квадратный стол, в углах которого расположено по сосуду. В каждый сосуд вставлено по селёдке, причём селёдка может располагаться вверх либо головой, либо хвостом. Снаружи расположение селёдок не видно. Али-Баба может засунуть руки в любые два сосуда, нащупать, как расположены селёдки, и установить их в любое положение (т. е. может оставить всё как было, а может перевернуть одну селёдку или обе). Эту операцию можно проводить несколько раз, однако после каждого раза стол начинает быстро вращаться, так что после его остановки невозможно определить, в какие именно сосуды Али-Баба засовывал руки. Дверь в пещеру открывается, если все селёдки стоят одинаково. Помогите Али-Бабе попасть в пещеру.

8.

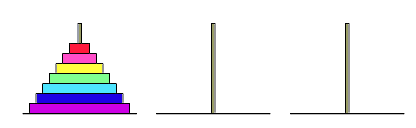
Ханойская башня. Головоломка «Ханойская башня» представляет собой три штырька, на один из которых нанизаны семь колец убывающих размеров, как показано на рисунке. Разрешается снимать по одному кольцу с любого штырька и нанизывать его на любой другой штырёк, но при этом запрещается класть большее кольцо поверх меньшего. Можно ли, соблюдая эти правила, переложить все кольца на другой штырёк?

9.

На бесконечном клетчатом листе бумаги 100 клеток закрашены в чёрный цвет, а все остальные — в белый. За один ход разрешается перекрашивать в противоположный цвет любые четыре клетки, образующие квадрат 2×2. Докажите, что за несколько ходов можно добиться того, что все клетки окажутся белыми тогда и только тогда, когда любая горизонталь и любая вертикаль содержит чётное число чёрных клеток.

10.

В каждой клетке бесконечного листа клетчатой бумаги записано натуральное число. При этом оказалось, что каждое число равно среднему арифметическому четырёх соседних чисел. Докажите, что все числа равны между собой.