Кружок 9-11 классов

Тема 2. Центр масс и его применение для решения геометрических задач

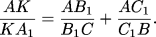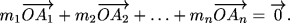
Задача. Старый пират зарыл клад на острове среди 20 деревьев. После этого он написал завещание, в котором указал, как искать клад: надо встать к первому дереву, пройти половину расстояния до второго дерева, затем повернуть к третьему и пройти треть расстояния до него, и т. д., наконец, повернуть к двадцатому и пройти двадцатую часть расстояния до него. К сожалению, пират забыл указать, как занумерованы деревья! Сколько разных ям придётся выкопать потомкам пирата, чтобы всё-таки найти клад?

Ответ

Определение. Центром масс системы точек A₁, …, A_n с массами m₁, …, m_n (далее используется обозначение (A₁, m₁), …, (A_n, m_n)) называется такая точка O, что

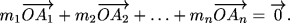
Обычно считается, что все массы положительны, однако вся теория работает и в случае, когда допускаются массы произвольного знака при условии, что m₁ + … + m_n ≠ 0.

Теорема 1 (о существовании). Для любой системы точек (A₁, m₁), …, (A_n, m_n) центр масс существует.

Доказательство

Доказательство. Пусть X — произвольная точка (начало координат). Тогда центром масс O рассматриваемой системы точек задаётся радиус-вектором:

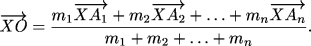
Теорема 2 (о единственности). Центр масс системы точек единствен.

Теорема 3 (о группировке масс). Центр масс системы точек (A₁, m₁), …, (A_n, m_n), (B₁, M₁), …, (B_k, M_k) совпадает с центром масс системы точек (A₁, m₁), …, (A_n, m_n), (C, M), где C — центр масс системы точек (B₁, M₁), …, (B_k, M_k), а M = m₁ + … + m_k.

С помощью центра масс можно легко доказать некоторые теоремы элементарной геометрии, например:

Теорема (о пересечении медиан). Медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении 2:1, считая от вершины.

Теорема (о пересечении биссектрис). Биссектрисы треугольника пересекаются в одной точке.

Подсказка

Теорема Чевы. На сторонах AB, BC и AC треугольника ABC взяты точки C₁, A₁ и B₁ соответственно. Тогда отрезки AA₁, BB₁ и CC₁ пересекаются в одной точке тогда и только тогда, когда

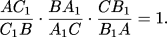
Такие отрезки AA₁, BB₁ и CC₁ называются чевианами.

Теорема Ван-Обеля. Пусть K — точка пересечения чевиан AA₁, BB₁ и CC₁ треугольника ABC. Тогда

Ещё несколько задач про центр масс

1.

Пусть ABCD — выпуклый четырёхугольник, K, L, M и N — середины сторон AB, BC, CD и DA соответственно. Докажите, что точка пересечения отрезков KM и LN является серединой этих отрезков, а также серединой отрезка, соединяющего середины диагоналей четырёхугольника ABCD.

2.

На сторонах BC и CD паралеллограмма ABCD взяты точки K и L так, что BK:KC = CL:LD. Докажите, что точка пересечения медиан ΔAKL лежит на диагонали BD.

3.

Докажите, что если у многоугольника есть несколько осей симметрии, то все они пересекаются в одной точке.

4.

Где находится центр масс правильного n-угольника с единичными весами в вершинах?

5.

Центрально симметричная фигура на клетчатой бумаге состоит из n «уголков» и k прямоугольников 1×4 (см. рисунок). Докажите, что n чётно.

Литература